Les ateliers

InforMATHique, Numérique et Robotique
Langage numérique : Algorithme et codage

Programmation d'une machine à dessin
Animateur·rice·s : Jean Cordier
Cycle : du CE2 à la 4eme
Les participants devront organiser les déplacements d'une tête robotisé tenant un feutre afin de faire un dessin, puis de les coder sur un ordinateur. L'organisation des idées se fait avec de petites cartes aimantées, et le codage en texte (comme les vrais programmeurs!!). Le groupe repartira avec un dessin issu de la machine.

Atelier objets connectés
Animateur·rice·s : Simone Ferrecchia, Alejandra Forero
Cycle : à partir de 13 ans
Dans cet atelier autour des objets connectés les participants explorent des dispositifs électroniques diy connectés à internet, ils/elles découvrent la programmation informatique, manipulent et apprennent à reconnaitre des composants électroniques.
Il sera également possible d'aborder des questions liées à la vie privé et à la sécurité des objets connectés.

Atelier Code en Bois
Animateur·rice·s : Marc Agenis
Cycle : Il est nécessaire de savoir lire pour réaliser l'atelier.
Age recommandé: 7 ans à 14 ans.
Venez vous initier à l'algorithmique "déconnectée" et tenter de résoudre des défis en imaginant un programme à l'aide d'instructions en bois.

Mission Cryptographie
Animateur·rice·s : Pascal Lafourcade
Cycle : Lycée première et terminale.
A travers des énigmes ludiques nous allons vous faire découvrir la cryptographie.

Mosaique LEGO(r)
Animateur·rice·s : Nicolas Charnay
Cycle : Tous public a partir de 5ans
Fabriquons ensemble une grande fresque en LEGO(r).
Code menteur
Animateur·rice·s : Candice Bernard
Cycle : De 7 à 18 ans
Meilleure stratégie face à un menteur : il choisit une carte 00 01 10 ou 11 et on doit la deviner en posant des questions fermées mais il a le droit de mentir une fois. Quel est le nombre minimal de question que l’on doit poser pour connaître à tous les coups la carte ? C’est une introduction à la théorie de l’information, à savoir la restitution de message en dépit d’éventuelles erreurs de transmission.
Les algorithmes génétiques
Animateur·rice·s : Hugo Marsan
Cycle : À partir de 11 ans.
Découverte du principe d’algorithme génétique à travers un jeu.

Programmation carte microbit
Animateur·rice·s : Pascal Vincent
Cycle : CM2, college
Présentation des cartes et de l’interface de programmation.
Mise en activités des élèves, deux par ordinateur (hors ligne) avec deux cartes micro:bit.
Mise en activités des élèves, deux par ordinateur (hors ligne) avec deux cartes micro:bit.

Communiquer avec un robot
Animateur·rice·s : Benidicte Artola
Cycle : Dès Cycle 1
Manipuler et programmer des Bluebot et des Thymio
Jeux Mathématiques
Pour le plaisir des mains et de la tête !

Mathémagique
Animateur·rice·s : Clément Sire
Cycle : 10 ans et + (collège ou lycée)
Mathémagique : Tours de Magie... ou de Mathématiques ?

Math & magie
Animateur·rice·s : Dominique Souder
Cycle : Tout niveau scolaire : primaire, collège, lycée.
Il s'agit de "motiver les élèves et faire vivre les mathématiques grâce à la mathémagie". On utilise la curiosité, puis l'émerveillement pour que les élèves s'investissent davantage en maths, prennent confinence en eux et deviennent créatifs. Les tours sont variés : cartes, dés, découpages, ficelles, matériels originaux créés (nécessitant papier, crayon) de coût nul.

Maths Précolombiens
Animateur·rice·s : Isabelle Turmo, Jean Schubmelhl
Cycle : atelier pour le tout public
Les civilisations précolombiennes maîtrisaient des connaissances comme :
les mathématiques, l'astronomie, l'architecture, l'agronomie...
3 pôles sont présentés : manipulation autour de la numération mayas
manipulation autour des pyramide aztèques
manipulation autour des quipus incas
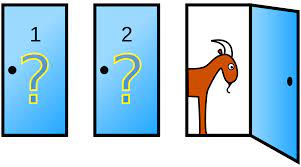
Jeu de Monty Hall
Animateur·rice·s : Danièle Gérard
Cycle :
Comment optimiser ses chances de trouver la bonne porte parmi trois, quand une porte s'ouvre sur un trésor et deux sur des chèvres? Un indice sera-t-il aidant?

Magimatique
Animateur·rice·s : Jean-Baptiste Aubin
Cycle :
Les mathématique regorgent de propriétés étonnantes. Ces propriétés, souvent simples, peuvent permettre de créer des tours de magie, que ce soit par exemple pour calculer mentalement à une vitesse hors du commun ou faire des prédictions (apparemment) inatteignables par la logique pure. L'atelier sera l'occasion de découvrir certains de ces tours et de se familiariser avec certaines des techniques de calculateurs prodiges.
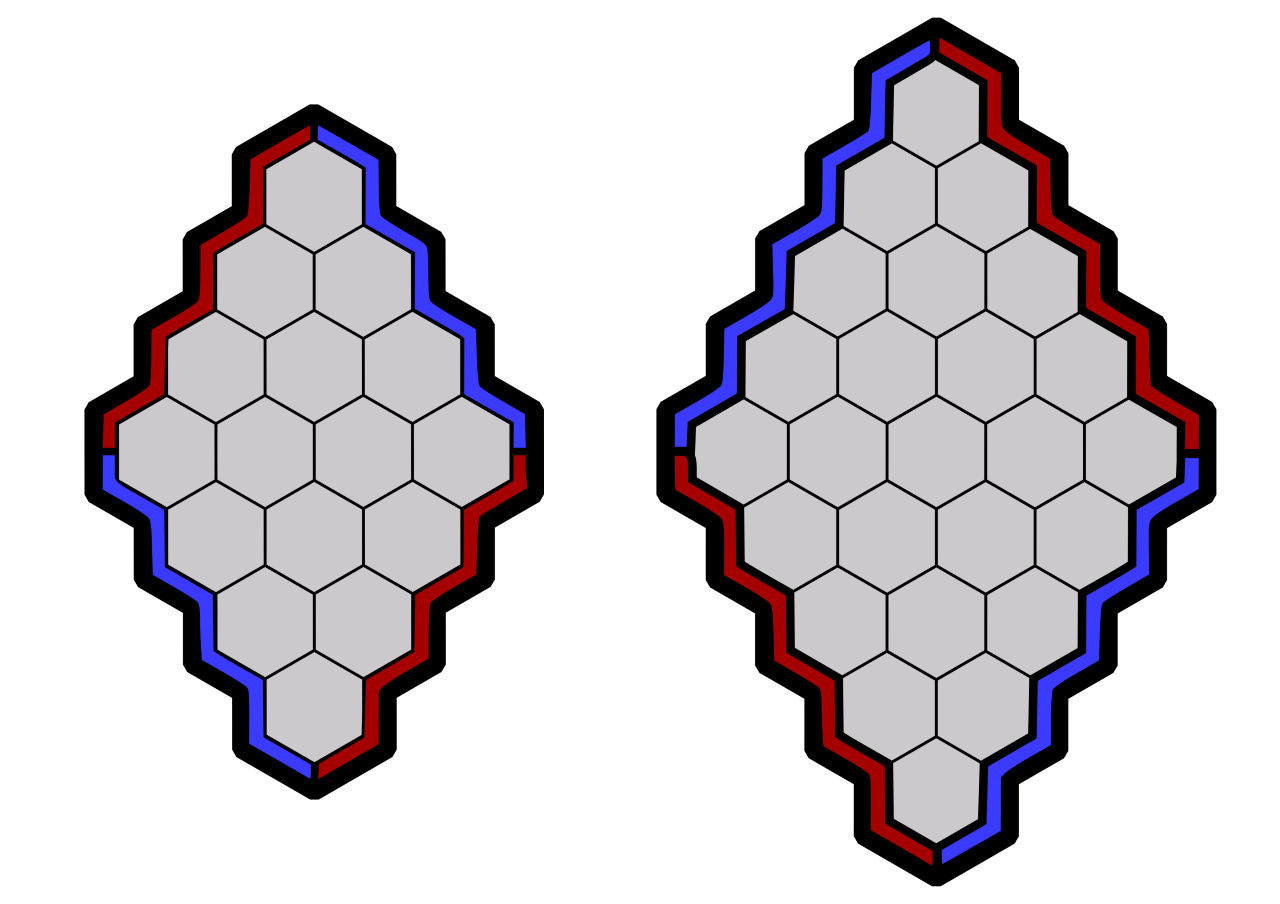
Hex-aequo ?
Animateur·rice·s : Owen Rouillé
Cycle : collège et lycée
Le but de cet atelier est d'entrer dans le monde de la Théorie des Jeux : le Jeu de Hex. Il s'agit d'un jeu introduit par Piet Hein en 1942. Sur un plateau en forme de losange pavé par des cases carrées, chacun des joueurs posent à tour de rôle un pion de sa couleur sur une case libre. Le but du joueur est de relier les côtés opposés de sa couleur par un chemin ininterrompu de pions.
Nous laisserons le temps aux lycéens et lycéennes de se familiariser avec le jeu en jouant des parties contre l’animateur et/ou entre eux sur des plateaux de différentes tailles. Puis soit cela viendra d'eux-mêmes, deux questions leurs seront posées si elles ne viennent pas d’eux-mêmes.
Y a-t-il toujours un gagnant ?
L'un des deux joueurs peut-il toujours gagner ?

Simplement complexe
Animateur·rice·s : Bruno Teheux, Ann Kiefer, Laurent Loosveldt
Cycle : De 7 à 99 ans.
À partir d'outils très simples, les mathématiques permettent de construire des structures d'une variété infinie. Au travers de jeux, explorerez un univers mathématique maintenu en perpétuelle construction. Sans formalisme, il ne reste que le plaisir de la découverte, de la réflexion et du partage.

Jeux APMEP
Animateur·rice·s : Yves Farcy, Bruno Alaplantive
Cycle : 13-17 ans
Venez découvrir les jeux mathématiques des revues de l'APMEP. Se prendre au jeu, faire travailler ses méninges pour résoudre les différents jeux

Découverte : jeux de société modernes
Animateur·rice·s : Annabel Fourcade
Cycle :
Exit Monopoly, Cluedo ou autres classiques et place à une multitude de jeux de société : venez jouer en famille, entre amis ou solo pour découvrir des jeux coopératifs, de stratégie, d'ambiance, de réflexion, de cartes et bien d'autres.

KIMIK
Animateur·rice·s : Anne Gomez
Cycle : Ce jeu ne demande aucun prérequis et est accessible à tous, petits et grands.
KIMIK est un jeu sur la thématique de la chimie.
A l’aide des cartes « Eléments » les joueurs doivent assembler et former le maximum de « Molécules » pour gagner des points. Ce jeu ne demande aucun prérequis et est accessible à tous, petits et grands.

Le magicien débutant
Animateur·rice·s : Pierre Bonnet
Cycle :
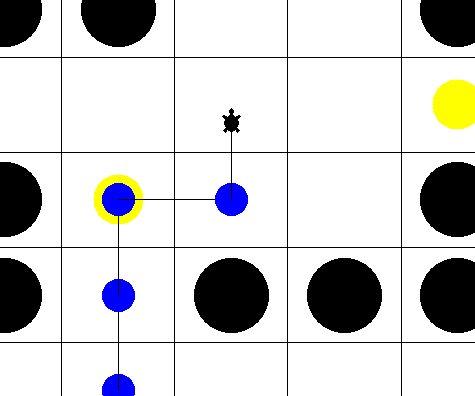
Comment se déplacer en le moins d’étapes possibles dans une situation où chaque coup est incertain ?
Au moyen d’un simple plateau et d’un dé, l’atelier consistera à chercher une stratégie de déplacement rapide pour un magicien doué de téléportation (incertaine).
Au moyen d’un simple plateau et d’un dé, l’atelier consistera à chercher une stratégie de déplacement rapide pour un magicien doué de téléportation (incertaine).
Intelligence Artificielle

Tout ce que vous avez toujours connaître sur l'IA et que vous n'avez osé demander
Animateur·rice·s : Samuel Nowakowski
Cycle : tout public
Samuel Nowakowski, maître de conférence à l’Université de Lorraine et chercheur au laboratoire Loria, animera une conférence

Les algorithmes génétiques
Animateur·rice·s : Hugo Marsan
Cycle : À partir de 11 ans.
Découverte du principe d’algorithme génétique à travers un jeu.

Jouer contre une IA débranchée
Animateur·rice·s : Bruno Lafrance
Cycle :
Un atelier où on apprend à jouer au jeu de Nim à une machine faite de ....boites d'allumettes

IA et Femmes Scientifiques
Animateur·rice·s : Céline Chantry-Darmon
Cycle : A partir de 6 ans (il faut juste que les enfants sachent lire).
Dans cet atelier, vous découvrirez des femmes scientifiques et leurs travaux qui ont marqué l'histoire. Nous aborderons également l'intelligence Artificielle, ses applications dans notre vie et les nouveaux outils de génération de texte et d'images, comme ChatGPT3 et DALL.E2 qui ont été utilisé pour généré ce jeu.

Arts et Maths
Des artistes au coeur de la science

La beauté des mathématiques à travers l'origami
Animateur·rice·s : Marie Ohye
Cycle : dès le Cycle 2
L’origami, l’art du pliage du papier, du japonais Oru (plier) et Kami (papier). Les pliages d’origami peuvent être utilisés en mathématiques pour procéder à des constructions géométriques. Selon les méthodes de pliages utilisées, on obtient des procédés plus riches que ceux propres à la règle et au compas. De l’origami à l’origami modulaire, en partant d’une ou plusieurs feuilles carrées, vous réaliserez une production collaborative géométrique et artistique!
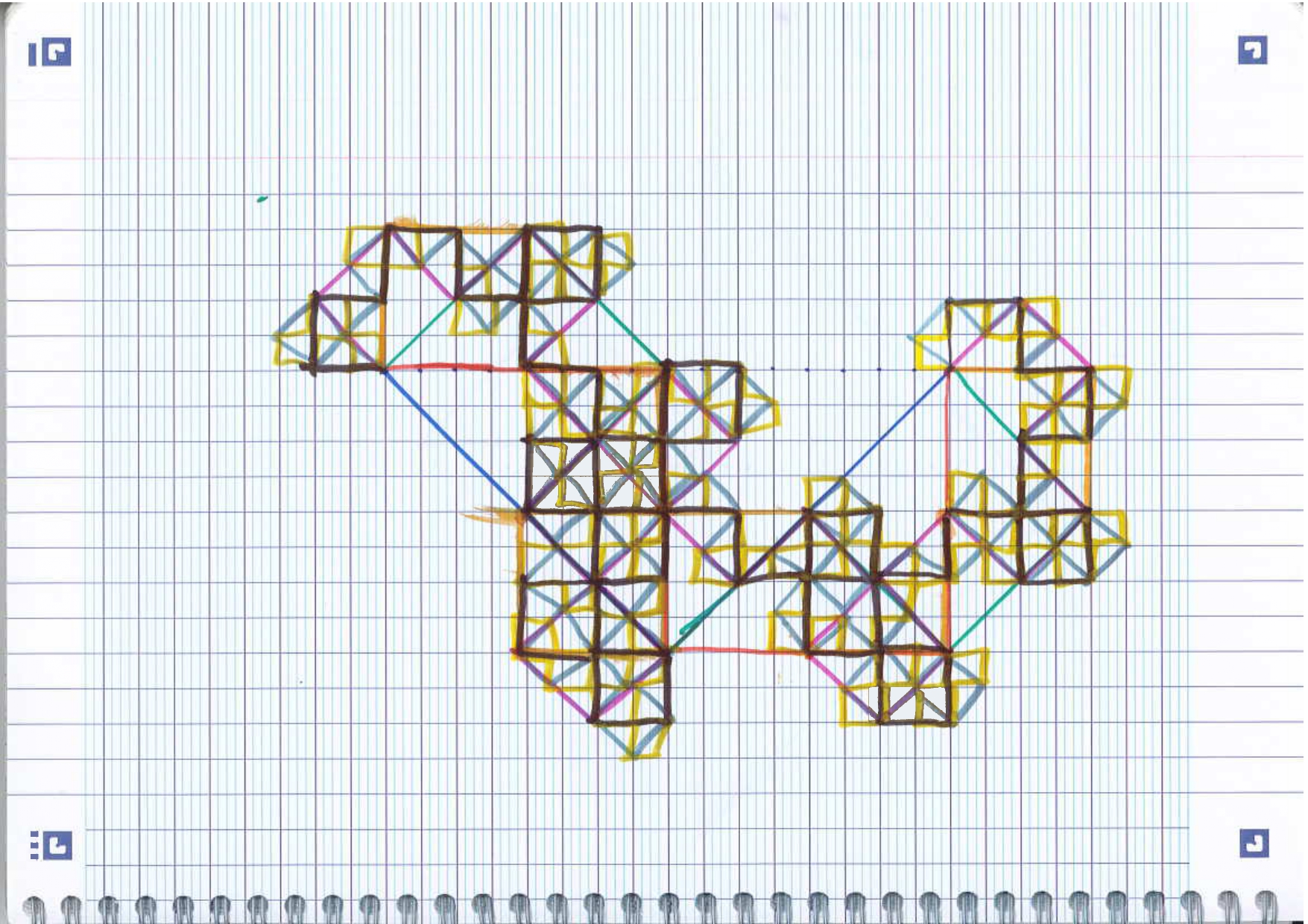
Dragon fractal et compagnie
Animateur·rice·s : Stéphane Génieys
Cycle : Tout public. Age : les maternelles sont possibles mais risquent de s'ennuyer au bout d'un moment. A partir du primaire pas de problème. Pas de limite supérieure.
Dans cet atelier, on dessinera collectivement un dragon fractal, aux feutres et à la règle. A la fin du festival, tous les dragons fractals feront un grand dragon.

Mandalas Mathématiques
Animateur·rice·s : Agnès Rigny
Cycle : CM2 et plus
Réalisation de mandalas mathématiques.

Exposition la beauté des formules de maths
Animateur·rice·s : Agnès Rigny
Cycle : Tout public
Exposition d'Agnès Rigny: la beauté des formules de maths. Textes d'Emmanuel Amiot.

Mathématiques en musique
Animateur·rice·s : Danièle Gérard
Cycle : A destination uniquement des élèves de CM2 et de 6e.
A partir d'un canon à trois voix chanté au début de l'atelier, sont abordées la notion de codage du langage musical ainsi que la notion de rythme.
Puis en observant des partitions, différentes fractions sont mises en évidence ainsi que des égalités de fractions.

Ma carte en 3D
Animateur·rice·s : Anne Lapouge
Cycle : De la grande section de maternelle à la 3ème.
Le contenu de l'atelier est adapté en fonction de l'âge et du niveau.
Quand les mathématiques rencontrent l'art, l'écriture scientifique et la créativité ; cela peut donner, en autre chose, une carte en 3D personnalisée et personnalisable à souhait, à volonté.

Tiens-toi à carreau, l'art de l'azulejo
Animateur·rice·s : Laura Drifford
Cycle : L'atelier peut être proposé de la Maternelle au Lycée
En effet, plusieurs déclinaisons permettent à notre animatrice de s'adapter à la tranche d'âge concernée
Tiens-toi à carreaux l'art de l'azulejo
Créations de motifs andalous à l'aide des techniques traditionnelles des artisans d'autrefois. A partir de traits et de cercles, l'azulejo apparaît !
Un atelier haut en couleur pour découvrir la géométrie autrement

Cube ajouré Origami
Animateur·rice·s : MONIQUE DUPUY
Cycle : Vu la dextérité, pour public motivé, enfants à partir de 4ème ?
Cube Origami : à partir de 6 feuilles carrées, à couper en deux, puis à plier et assembler. On obtient un cube à faces ajourées par des carrés.
Niveau de difficulté "moyenne". Demande de la patience et de la dextérité ... pour être exécuté en 50 minutes !

Mosaique LEGO(r)
Animateur·rice·s : Nicolas Charnay
Cycle : Tous public a partir de 5ans
Fabriquons ensemble une grande fresque en LEGO(r).

Hitomesashi
Animateur·rice·s : Brigitte Chaput
Cycle : Élèves de cycles 3
Broderies Hitomesachi sur des plaques de carton rigide perforées. Réalisation de motifs géométriques.
Anamorphose
Animateur·rice·s : Nathalie Braun
Cycle : 13 ans- 15 ans
1. Présentation d'anamorphoses
2. Les élèves vont réaliser des anamorphoses cylindriques à l'aide d'un miroir cylindrique.
2. Les élèves vont réaliser des anamorphoses cylindriques à l'aide d'un miroir cylindrique.

Atelier Art de KZO
Animateur·rice·s : Jean Paul CAZAUX
Cycle :
KZO de son vrai nom Jean Paul CAZAUX , réside et travaille à Muret depuis 1966.
Diplômé des Industries et Arts Graphiques de Toulouse, Grenoble et Paris à l’école supérieur Estienne, il a commencé ses premières œuvres apparentées à l’Art Optique à l’Age de 21 ans.
Après une longue pause, il a ressenti le besoin de se recentrer et de renouer avec sa passion qu’il aborde aujourd’hui comme une évidence et un moyen de s’évader.
« Je travaille principalement à l’encre de chine noire avec règle et compas sur carte graphique blanche et utilise la peinture à vitrail pour la couleur.
Deux thèmes sont traités : le graphisme et le figuratif en 3 phases de travail La créativité mentale, un tracé précis par la maitrise des outils de calculs et pour finir le remplissage par la méditation.
Au début, Je n’ai pas une idée précise du résultat final. L’œuvre se construit par mes bagages mathématiques sans brouillons et ce sentiment de découverte et parfois de surprise participe au plaisir de dessiner par les maths et de transmettre cet art aux différentes générations par des ateliers aux particuliers et aux étudiants dans les Lycées et collèges. »
Plus d'informations sur KZO DES ARTISTES.
Diplômé des Industries et Arts Graphiques de Toulouse, Grenoble et Paris à l’école supérieur Estienne, il a commencé ses premières œuvres apparentées à l’Art Optique à l’Age de 21 ans.
Après une longue pause, il a ressenti le besoin de se recentrer et de renouer avec sa passion qu’il aborde aujourd’hui comme une évidence et un moyen de s’évader.
« Je travaille principalement à l’encre de chine noire avec règle et compas sur carte graphique blanche et utilise la peinture à vitrail pour la couleur.
Deux thèmes sont traités : le graphisme et le figuratif en 3 phases de travail La créativité mentale, un tracé précis par la maitrise des outils de calculs et pour finir le remplissage par la méditation.
Au début, Je n’ai pas une idée précise du résultat final. L’œuvre se construit par mes bagages mathématiques sans brouillons et ce sentiment de découverte et parfois de surprise participe au plaisir de dessiner par les maths et de transmettre cet art aux différentes générations par des ateliers aux particuliers et aux étudiants dans les Lycées et collèges. »
Plus d'informations sur KZO DES ARTISTES.

Maths Vivantes
Et vive les maths!

Magimatique
Animateur·rice·s : Jean-Baptiste Aubin
Cycle :
Les mathématique regorgent de propriétés étonnantes. Ces propriétés, souvent simples, peuvent permettre de créer des tours de magie, que ce soit par exemple pour calculer mentalement à une vitesse hors du commun ou faire des prédictions (apparemment) inatteignables par la logique pure. L'atelier sera l'occasion de découvrir certains de ces tours et de se familiariser avec certaines des techniques de calculateurs prodiges.

Contes mathématiques
Animateur·rice·s : Marie Lhuissier
Cycle : Le conte *Les diamants parfaits* est adapté de la 6e au lycée. (public familial : à partir de 8 ans)
Les contes *La clef magique*, La faiseuse de neige* et *Conte Tout Droit* sont adaptés du CP à la 5e. (public familial : à partir de 6 ans)
Le conte *Lune* est adapté de la grande section de maternelle au CE2. (public familial : à partir de 4 ans)
Marie Lhuissier, conteuse-mathématicienne, et Alex Dandlò, musicien, vous invitent à découvrir ou redécouvrir des objets mathématiques étonnants au travers de contes originaux. Accompagné par la guitare, l'accordina ou le tambour argentin, chaque conte invite à suivre un personnage en quête de beauté, de liberté ou connaissance qui, au cours de son parcours, va se retrouver en position de mathématicien, en prise avec un objet nouveau, beau et fascinant. Des contes mathématiques sans nombres et sans technique, sensibles et poétiques, pour dire que les maths, ce n'est pas que du calcul, et que les mathématiques sont un lieu de beauté et de créativité. Pour donner envie à chacun, aussi, de comprendre et de de fabriquer lui-même l'objet mathématique du conte

Polyrythmie : la musique des nombres.
Animateur·rice·s : Maxence Brévard
Cycle : A partir de la sixième.
Le polyrythme, c’est un outil dont le musicien se sert pour provoquer l'envie de danser. C’est un outil rythmique puissant qui est caché dans ton corps et que la démarche mathématique permet révéler. Musicien ou pas, viens apprendre à inventer des polyrythmes !
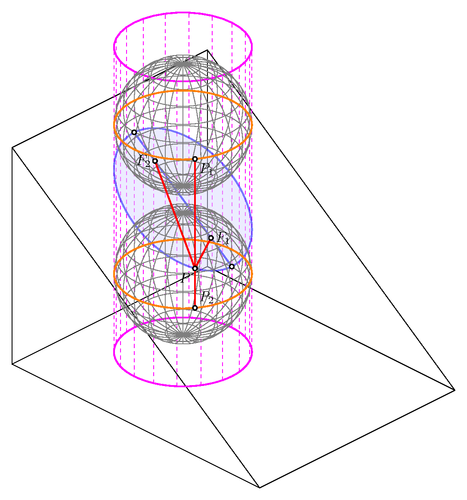
MATHS et Espace
Tout en mouvement

La courbure, qu'est-ce que c'est ?
Animateur·rice·s : François Gaudel
Cycle :
Quelle est la différence entre un objet plat et un objet courbe ? La terre est-elle plate ? Notre espace est-il plat ou courbe ? Comment le savoir alors qu'on ne peut pas en sortir ni prendre le temps d'en faire le tour, s'il y en a un ?

Le cube retournable
Animateur·rice·s : Monique Dupuy
Cycle : Convient à tout public ... pour les enfants, au moins CM-2
Patron de cube, pliable dans un sens ou dans l'autre. A découper et décorer.

Cube ajouré Origami
Animateur·rice·s : MONIQUE DUPUY
Cycle : Vu la dextérité, pour public motivé, enfants à partir de 4ème ?
Cube Origami : à partir de 6 feuilles carrées, à couper en deux, puis à plier et assembler. On obtient un cube à faces ajourées par des carrés.
Niveau de difficulté "moyenne". Demande de la patience et de la dextérité ... pour être exécuté en 50 minutes !

Prison
Animateur·rice·s : Arnaud Chéritat
Cycle : À partir de la 5e
Quelle drôle de prison. Il n’y a pas de porte aux cellules. On vous y demande d’attacher votre chaîne aux 4 barreaux de la fenêtre. Puis le gardien vient en scier un. Serez vous magicien et perspicace pour vous libérer ?

Les nombres par delà les étoiles
Animateur·rice·s : Maël Ricard, Agnès Viel, Jean Kellens, Lilou Renaud
Cycle : Cette animation est adaptée à tous les publics, dès 6/7 ans.
Venez découvrir à travers le système solaire les dimensions de ce qui nous entoure. De la taille du Soleil à la distance entre Saturne et la Terre, vous connaitrez tout de l'environnement de notre belle planète bleue.

LittéraMaths

Codes Secrets
Animateur·rice·s : Isabelle Turmo, Jean Schubmehl
Cycle : cycle 3 - début cycle 4 (du CE2 à la 5ème)
L'atelier Codes secrets, est une initiation à la cryptologie mono-alphabétique.
Chiffrer et déchiffrer avec le code César, le carré de Polybe, le Pig-Pen ou bien la scytale spartiate, autant de façon de coder et décoder des messages qui doivent rester secrets.

Contes mathématiques
Animateur·rice·s : Marie Lhuissier
Cycle : Le conte *Les diamants parfaits* est adapté de la 6e au lycée. (public familial : à partir de 8 ans)
Les contes *La clef magique*, La faiseuse de neige* et *Conte Tout Droit* sont adaptés du CP à la 5e. (public familial : à partir de 6 ans)
Le conte *Lune* est adapté de la grande section de maternelle au CE2. (public familial : à partir de 4 ans)
Marie Lhuissier, conteuse-mathématicienne, et Alex Dandlò, musicien, vous invitent à découvrir ou redécouvrir des objets mathématiques étonnants au travers de contes originaux. Accompagné par la guitare, l'accordina ou le tambour argentin, chaque conte invite à suivre un personnage en quête de beauté, de liberté ou connaissance qui, au cours de son parcours, va se retrouver en position de mathématicien, en prise avec un objet nouveau, beau et fascinant. Des contes mathématiques sans nombres et sans technique, sensibles et poétiques, pour dire que les maths, ce n'est pas que du calcul, et que les mathématiques sont un lieu de beauté et de créativité. Pour donner envie à chacun, aussi, de comprendre et de de fabriquer lui-même l'objet mathématique du conte

Des Maths Connectées
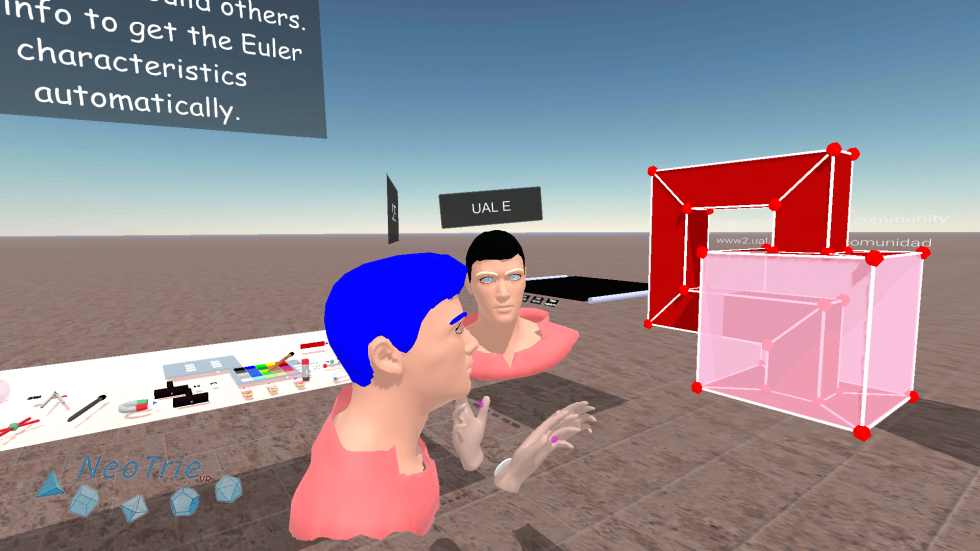
Géométrie en réalité virtuelle
Animateur·rice·s : José Luis Rodríguez
Cycle : 8-18 annéés
Dans cet atelier, les élèves pourront entrer dans le métavers de Neotrie VR, un monde de réalité virtuelle qui leur permet de créer, de manipuler et d'interagir avec des objets géométriques en 3D. Ils le feront avec des casques Meta Quest dans un environnement multijoueur, où ils pourront pratiquer certaines des activités conçues dans le cadre du projet Erasmus plus Geometrician's Views.

Atelier objets connectés
Animateur·rice·s : Simone Ferrecchia, Alejandra Forero
Cycle : à partir de 13 ans
Dans cet atelier autour des objets connectés les participants explorent des dispositifs électroniques diy connectés à internet, ils/elles découvrent la programmation informatique, manipulent et apprennent à reconnaitre des composants électroniques.
Il sera également possible d'aborder des questions liées à la vie privé et à la sécurité des objets connectés.

Maths et Sport
Les Maths pour se former

Echecs et mathématiques
Animateur·rice·s : Daniel Pélissier
Cycle :
Vous êtes conviés au mariage heureux de la « reine des sciences » et du « roi des jeux ». Venez en famille résoudre des casse-têtes, réfléchir aux célèbres problèmes des 8 reines ou du cavalier par la pratique et la théorie, découvrir la légende de Sissa, maîtriser les tempêtes sur l’échiquier ou tout simplement vous divertir et jouer !

Learn-O : Faire des maths . . . un jeu d'enfants
Animateur·rice·s : Xavier Dufour
Cycle : maternelles
primaires
collèges
Avec Learn-O, on aborde les apprentissages de façon originale et très stimulante.
Un doigt électronique, une carte de défi et c'est parti pour une multitude d'exercices sur des thématiques variées !
On bipe des balises et quand on a fini, l'ordinateur vérifie immédiatement notre parcours. En plus, si on se trompe, on peut voir où et aller nous corriger. Ainsi, on est toujours en réussite, donc valorisés. Et on repart de la sorte en multipliant les circuits.
Nous sommes vraiment acteurs de notre progression, placés en situation d'autonomie en sollicitant la tête et les jambes, dans le respect de nos rythmes propres. En plus, si on veut, on peut courir.
Cet outil s'adresse à tous, dès l'âge de trois ans.
Learn-O 31-82 propose différentes configurations, plusieurs modes d'activités et de nombreuses variables permettant de multiplier les façons d'apprendre et d'utiliser la grande quantité d'exercices proposés, de façon adaptée à chaque objectif, chaque public et chaque participant.
L'essayer, c'est l'adopter !

Découverte du Pilates
Animateur·rice·s : Anne Gomez
Cycle :
Le Pilates est une méthode de renforcement des muscles profonds, responsables de la posture. Les muscles profonds sont les muscles du centre, qui se situent entre les côtes et le bassin, et tout autour de la colonne vertébrale (abdominaux, plancher pelvien et les muscles du dos).

Maths et la planète Terre
Maths : Ma planète au service de la citoyenneté

Ombres et projections
Animateur·rice·s : Richard Kelly
Cycle : Grand public et scolaires à partir du 6ème.
Construire une forme avec des ombres incompatibles. Trouver les différentes ombres d'un cube ou des triangles. Et si la terre était une pyramide? Explore le monde des ombres.

Les nombres par delà les étoiles
Animateur·rice·s : Maël Ricard, Agnès Viel, Jean Kellens, Lilou Renaud
Cycle : Cette animation est adaptée à tous les publics, dès 6/7 ans.
Venez découvrir à travers le système solaire les dimensions de ce qui nous entoure. De la taille du Soleil à la distance entre Saturne et la Terre, vous connaitrez tout de l'environnement de notre belle planète bleue.

ExploraMaths
Les Maths vous en mettent plein les yeux

Atelier de construction libre Lego
Animateur·rice·s : Pierre Aubry
Cycle : A partir de 2 ans sous la surveillance d'adultes accompagnants
Un maximum de briques pour un maximum de constructions : laissez parler votre imagination

Simplement complexe
Animateur·rice·s : Bruno Teheux, Ann Kiefer, Laurent Loosveldt
Cycle : De 7 à 99 ans.
À partir d'outils très simples, les mathématiques permettent de construire des structures d'une variété infinie. Au travers de jeux, explorerez un univers mathématique maintenu en perpétuelle construction. Sans formalisme, il ne reste que le plaisir de la découverte, de la réflexion et du partage.

Exposition Arts et maths de Geometrician's View (GV)
Animateur·rice·s : Les Maths en Scènes
Cycle :
Le projet KA225-SCH-095534, « Vues du géomètre » (GV) est une coopération internationale dans le domaine de l'éducation. L'objectif de l'initiative est de permettre aux élèves de la maternelle au lycée d'explorer la culture mathématique à travers l'art et la science.
Des partenaires de 6 pays différents sont invités à échanger des approches innovantes en matière d'enseignement des mathématiques, les étudiants sont invités à créer des livrables collaboratifs à l'intersection entre les mathématiques et les arts. L'initiative comprend une formation internationale du personnel ouverte aux membres des organisations participantes, ainsi que des événements multiplicateurs pour diffuser les résultats du projet (Le site du projet).
Le consortium GV prévoit de produire un certain nombre de résultats tangibles, notamment des supports pour des expositions mobiles sur les mathématiques et les arts.

IMAGINARY
Animateur·rice·s : Les Maths en Scène
Cycle :
Venez découvrir des poster saisissants et des modèles en 3D pour toucher les mathématiques.
IMAGINARY is a platform for open and interactive mathematics. It features a variety of content that can be used in schools, at home, in museums, at exhibitions or for events and media activities.
The main contents of IMAGINARY are its interactive programs and its picture galleries.

Magimathique
Animateur·rice·s : Exposition de la MMI
Cycle :
Magique ? Presque, mathématique !
Une exposition inédite mixe magie et science pour émerveiller toute la famille.

Imaginaire mathématique
Animateur·rice·s : Samuel Lelièvre, Alba Málaga
Cycle :
Un espace dédié aux images, objets (impression 3D, découpe lame ou laser, etc), films, logiciels, proches de la recherche mathématique, en puisant
du contenu sous licence libre dans des plateformes comme «IMAGINARY», «Kits math» et «Thingiverse»:
https://IMAGINARY.org
https://kits.math.cnrs.fr
https://www.thingiverse.com/search?q=mathematics
Rencontre

Tout ce que vous avez toujours connaître sur l'IA et que vous n'avez osé demander
Animateur·rice·s : Samuel Nowakowski
Cycle : tout public
Samuel Nowakowski, maître de conférence à l’Université de Lorraine et chercheur au laboratoire Loria, animera une conférence

Conférence Hugo Duminil-Copin
Animateur·rice·s : Hudo Duminil-Copin
Cycle : 15-18 ans
Conférence du mathématicien Hugo Duminin-Copin, médaille Fields 2022

Comment multiplier en ne connaissant que la table de 2 ?
Animateur·rice·s : Aurélien Alvarez
Cycle : 6ème
Conférence d'Aurélien Alvarez, professeur à l'École normale supérieure de Lyon.
Nous verrons une méthode venant d’Éthiopie et d’Égypte qui permet de multiplier deux nombres quelconques uniquement en faisant des multiplications par 2.
Nous verrons une méthode venant d’Éthiopie et d’Égypte qui permet de multiplier deux nombres quelconques uniquement en faisant des multiplications par 2.

Conférence de Diarra Fall
Animateur·rice·s : Diarra Fall
Cycle :
“Traitement d’images: mathématiques, algorithmique et intelligence artificielle”
Les images sont omniprésentes dans nos vies, que cela soit des images statiques (photos), ou dynamiques (vidéos). Derrière ces images, se cachent beaucoup de mathématiques, des plus simples aux plus complexes, que cela soit pour la reconstruction (permettant d’avoir les images) ou pour le traitement (portant sur les images déjà reconstruites). Dans cet exposé, on verra dans un premier temps comment des mathématiques simples permettent de traiter des images (changement de luminosité, de contraste, recalage, recollage, débruitage etc.)
Dans un second temps, on montrera des traitements basés sur des mathématiques et algorithmes plus sophistiqués, et l’apport de l’intelligence artificielle dans ce domaine.
Diarra FALL Personal web page
Les images sont omniprésentes dans nos vies, que cela soit des images statiques (photos), ou dynamiques (vidéos). Derrière ces images, se cachent beaucoup de mathématiques, des plus simples aux plus complexes, que cela soit pour la reconstruction (permettant d’avoir les images) ou pour le traitement (portant sur les images déjà reconstruites). Dans cet exposé, on verra dans un premier temps comment des mathématiques simples permettent de traiter des images (changement de luminosité, de contraste, recalage, recollage, débruitage etc.)
Dans un second temps, on montrera des traitements basés sur des mathématiques et algorithmes plus sophistiqués, et l’apport de l’intelligence artificielle dans ce domaine.
Diarra FALL Personal web page

IA et Femmes Scientifiques
Animateur·rice·s : Céline Chantry-Darmon
Cycle : A partir de 6 ans (il faut juste que les enfants sachent lire).
Dans cet atelier, vous découvrirez des femmes scientifiques et leurs travaux qui ont marqué l'histoire. Nous aborderons également l'intelligence Artificielle, ses applications dans notre vie et les nouveaux outils de génération de texte et d'images, comme ChatGPT3 et DALL.E2 qui ont été utilisé pour généré ce jeu.
