Broder autour de Code en Bois
Écrit par Marc Agenis, gérant de l’entreprise Code en Bois, entrepreneur dans l’éducation et le numérique.
Les lecteurs fidèles de ce site auront sans doute déjà vu passer au détour d’un tweet des images de petites briques colorées avec des instructions dessus. Il s’agit des tuiles « code en bois » mises au point par une entreprise clermontoise avec laquelle l’association LMES (Les Maths en Scène) collabore depuis 2023.

C'est quoi « Code en bois » ?
Code en Bois, c’est comme du Scratch ou du Blockly sauf que tout se passe sans ordinateur, sans écran, sans électronique : les élèves créent des programmes sur leur table en assemblant leurs instructions et envoient un camarade exécuter le programme au tableau en déplaçant un personnage aimanté. Actions, boucles, conditions, tout y passe (il parait qu’on aura aussi les variables et les fonctions bientôt).
Ça démarre dès 7 ans et ça va jusqu’au début du cycle 4. Il y a beaucoup de possibilités d’activités pédagogiques qu’on peut réaliser autour de Code en Bois : faire déplacer un élève sur un carrelage, simuler une partie de football, chercher le programme le plus économe pour un défi donné, raconter des histoires, etc. Pour les plus âgés (cycle 4 et lycée), certains défis plus difficiles donnent même matière à pousser les enseignements en ouvrant sur la programmation Python.
Le Défi
Alors regardons ensemble comment nous pouvons « broder » autour du défi N°01 de la seconde extension (disponible ici).
Le défi est le suivant : un petit robot est placé sur la première case d’un chemin qui continue indéfiniment vers la droite de l’image. L’objectif est d’atteindre la case la plus éloignée possible sur ce chemin. Elémentaire ?

Non ! Car on ne dispose que d’une quantité limitée de briques en bois, à savoir :
- 4 instructions « avance »
- 2 boucles de répétition (qu’on pourra éventuellement imbriquer)
- 10 chiffres (de 0 à 9) pour spécifier le nombre d’itération de chaque boucle (on ne peut pas utiliser 2 fois le même chiffre).
Comme il pleuvait dehors nous sommes allés dans le gymnase et avons représenté le parcours avec des dalles de mousse emboitables de façon qu’un élève puisse facilement visualiser et exécuter le programme en se déplaçant.
Au bout de quelques minutes il semble assez évident pour les collégiens que la façon la plus efficace d’avancer loin est d’imbriquer les itérations pour « démultiplier » les 4 avance de cette façon :

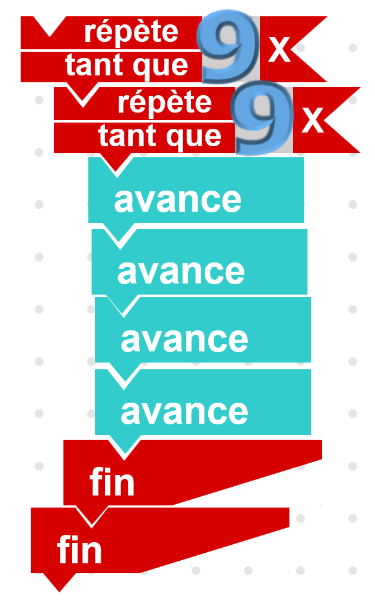
Évidemment, le voisin lui a fait remarquer qu’il avait dû chiper un « 9 » à un autre groupe car on n’en avait droit qu’à un seul. Il a alors rigolé en disant que non, pas du tout, c’était juste son 6 mis à l’envers. Na. On a dû accepter sa solution qui était quand même valide ; importance de la clarté des hypothèses et de l’énoncé !
Notre robot va alors pouvoir atteindre la 288ème case (si on suppose qu’il part de la case zéro), ou même la 324ème si on s’autorise le « hack » du 6 retourné au lieu d’un banal 8.
Si vous voulez représenter vous-même des emboîtements de briques, c’est possible sur ce tableau collaboratif : lien vers le tableau.
A partir de là, Emilie lève la main et demande, l’air naïve : « mais Monsieur, ça veut dire qu’on ne peut pas faire s’arrêter le robot entre la 288ème et la 324ème case ? ». Après un instant je réplique : « Non, en effet, cela semble impossible, il faudrait plus de briques ». Comme tout prof pour qui une question intéressante d’un élève amène à pousser plus loin un exercice, je réponds : « Est-ce que vous seriez capables de me donner la liste des cases sur lesquelles le robot peut effectivement s’arrêter ? ». Avec un nombre aussi limité de briques, il semblait intuitivement évident qu’on ne pourrait pas terminer le programme sur toutes les cases entre la N°1 et la N°324. Comment le prouver ? Il va falloir démarrer une console Python : par exemple Vittascience ou online-python.
Un premier élève fait remarquer qu’il y a deux grandes sortes de structures de programme possible : soit on fait deux boucles indépendantes, soit on imbrique les deux boucles. Le premier cas est plus facile à traiter : le maximum qu’on peut atteindre de cette façon est 36 (4*9 + 0*0), et on fait vérifier par « force brute » par les élèves qu’on peut réaliser tous les nombres entre 0 et 36 en mode #hackaton. C’est un peu comme « le compte est bon » et ils sont comme des fous !
La seconde structure, en imbriquant les boucles, laisse comme inconnues le choix des nombres d’itérations et l’emplacement des avances. Je les aide un peu en proposant le formalisme :
Case_atteinte = a + (X *(Y * c) + b), avec a le nombre d’avance en dehors des boucles, b dans la boucle externe et c dans la boucle interne, X, Y des nombres d’itérations entiers entre 0 et 9 tels que x !=Y.
Je demande ensuite : « quelle contrainte a-t-on sur a, b et c ? » et j’obtiens facilement la réponse : «la somme de a, b et c doit être inférieure ou égale à 4 ». On n’a en effet que 4 briques avance¸ mais on n’est pas obligé de les utiliser toutes. Je propose de faire tester par le programme toutes les combinaisons possibles de X, Y, a, b, c. On peut faire un bout de code pour trouver en premier lieu les combinaisons autorisées de a, b, et c :
for a in range(5):
for b in range(5):
for c in range(5):
if (a+b+c)<5:
combinaisons_abc.append((a, b, c))
print(combinaisons_abc) ;
print(len(combinaisons_abc))
L’idéal est de leur fournir le code avec les zones noires à deviner, car les notions de tuples ne sont pas toujours encore connues. C’est le premier M du modèle PRIMM (predict, run, investigate, modify, make). On a 35 combinaisons possibles. Vient ensuite notre programme principal, pareil on leur propose un programme à trous.
for combinaison in combinaisons_abc:
a, b, c = combinaison
for X in range(10):
for Y in range(10):
if Y != X:
set_cases_possibles.add(a + ( X *(Y * c) + b ))
print(sorted(set_cases_possibles));
print(len(set_cases_possibles)) # nombre total de possibilités
On explique aussi pourquoi on utilise un type de structure « set » pour pouvoir rajouter un nouvel item sans s’embêter à vérifier s’il est déjà présent ou pas. On obtient alors la liste des numéros de cases qu’on peut atteindre avec la structure imbriquée. Yeah ! Pour terminer, quelques questions pour départager les vainqueurs :
- Y-a-t ’il plus de numéros atteignables ou non atteignables ?
- Où les numéros non atteignables se situent-ils majoritairement (grands ou petits nombres) ?
- Quel est le plus petit numéro de case qui n’est pas atteignable ?
- Bonus philosophie : si on n’a pas de limite de briques ou de chiffres, jusqu’où peut-on aller ? Quelle partie du robot lâchera en premier ? 😊

PS
Si vous êtes intéressé(e) par le matériel Code en Bois, il y a plein de façons de s’en procurer et de tester :
- Acheter directement via le site www.codeenbois.fr
- Faire un projet CNR/NEFLE pour vous équiper et laisser libre cours à votre imagination
- Nous solliciter pour venir faire des ateliers intégralement financés par le pass culture !
- Demander une mallette de test pendant 2 mois
- Mettre des mini-kits code en bois dans vos sacs à maths…
