
Crée par Corina Murg, membre de l’association Les Maths En Scène et enseignante aux États-Unis.
La magie peut capter l’attention des élèves et a donc le potentiel d’engager leur esprit. Cet article vous invite à découvrir un tour de cartes qui montrera à vos élèves vos pouvoirs de mathémagicien.ne, tout en leur permettant d’utiliser leurs connaissances en algèbre.
Que la Magie Commence!

Vous allez utiliser un jeu de 52 cartes bien mélangé.
Pour cette activité, l’as vaut 1, le valet vaut 11, la dame 12 et le roi vaut 13.
Les Trois Étapes
1. Retournez la carte du dessus et placez-la sur la table. Utilisez la valeur de cette carte comme numéro de départ. Construisez une pile de cartes sur celle-ci, en ajoutant 1 au numéro de départ à chaque fois que vous posez une carte dessus. Arrêtez-vous à 13 et commencez une nouvelle pile.
- Par exemple, si la valeur de la carte de départ est 8, continuez à compter “9, 10, 11, 12 et 13,” en ajoutant chaque fois une nouvelle carte, quelle que soit sa valeur.
- Si la première carte d’une pile est un roi, ne posez rien dessus et commencez une nouvelle pile.
- Vers la fin, si vous n’avez plus assez de cartes pour faire une pile qui atteint 13, mettez de côté les cartes non-utilisées, face cachée.
2. Retournez les paquets. Demandez à vos élèves de sélectionner trois paquets et placez toutes les autres paquets avec les cartes non-utilisées. Comptez toutes les cartes non-utilisées.
3. Demandez à vos élèves de choisir encore deux paquets et retournez les cartes du dessus.
La Grande Révélation

La valeur de la carte du dessus du troisième paquet est inconnue,
mais après la troisième étape vous avez presque tous les indices nécessaires pour la deviner.
Pour la dernière étape, prenez une baguette magique et faites-la tourner trois fois … mais pas du tout! On ne va pas finir par magie, mais par algèbre:
L’étape secrète : De nombre de cartes non-utilisées soustrayez 10 et les valeurs sur les deux cartes retournées à l’étape 3.
Maintenant vous êtes vraiment prêt à révéler la valeur inconnue: elle correspondra au résultat de l’étape secrète !L
La Magie de l’Algèbre
Soit n le nombre de cartes non-utilisées. Soit a et b les nombres sur les deux cartes qu’on retourne à l’étape 3, et x la valeur inconnue. On connaît a et b, mais il faut deviner x.
Il y a au total 52 cartes. On peut écrire le nombre de cartes dans chaque paquet en fonction de la valeur de la carte du dessus. Puis on ajoute les trois paquets et les cartes non-utilisées.
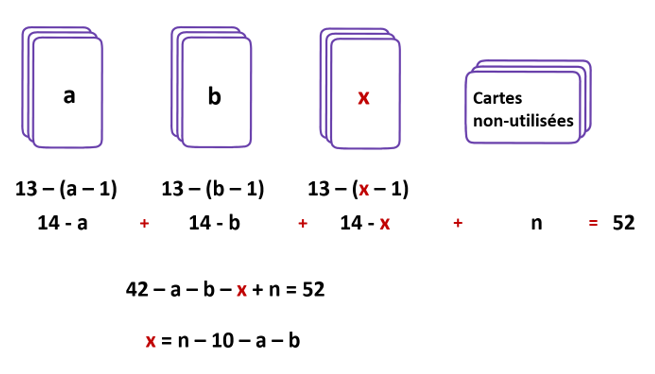
On voit que peu importe les piles qu’on sélectionne à l’étape 2 ou les cartes qu’on retourne à l’étape 3. Chaque fois la valeur inconnue sera égale au nombre de cartes non-utilisées moins 10 et les valeurs sur les deux cartes retournées à l’étape 3.
Comment aider vos élèves à découvrir le secret de cette magie ?

Le départ sera difficile, mais il faut donner aux élèves la chance de travailler en groupe et de jouer au tour de cartes plusieurs fois. Encouragez-les à partager leurs idées au sein de leur propre groupe et encouragez les groupes à échanger leurs découvertes.

Donnez-leur un indice seulement s’ils ne peuvent plus avancer. L’indice pourrait être sous la forme d’une question :
« Est-ce qu’on peut calculer le nombre de cartes dans les trois paquets sélectionnés ? »
« Quelle est la relation entre les paquets sélectionnés et les cartes non-utilisées ? Peut-on écrire une équation pour représenter cette relation? »

Une fois qu’ils se rendent compte qu’on doit soustraire 10 lors de l’étape secrète, demandez-leur de réfléchir au lien entre la valeur 10 et 13.

Encouragez les élèves à créer leur propre tour de cartes par changeant 13 avec un numéro différent. Ils devraient donc recalculer aussi la valeur à soustraire lors de l’étape secrète.
Profiter de leur curiosité !
La curiosité peut créer la motivation d’apprendre. Nos élèves sont intéressés par les activités ludiques et pour notre part on peut toujours essayez de les inclure dans nos cours de mathématiques. Ces activités peuvent stimuler la participation des élèves et assurer que la magie des mathématiques ne s’arrête jamais !

